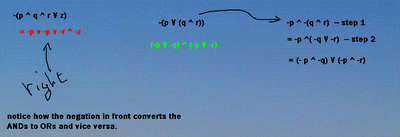
This went along with the chat window (names changed here):
Me: Allen, I'm going to have to do yours in two steps to see what gives... Me: notice how the negation (minus sign) attaches itself to each thing inside--just like normal algebra? Me: Now I've pulled the negation inside the parentheses using de Morgan's rule a second time Me: You got it. Me: See--I gave you the hard one! Allen: ok, i just didnt see the part about switching signs Me: It's very easy to miss stuff with logic. Kate: hi im back sry Me: Hi Kate, and hi Scott! Steve: hey, I'm trying to see what we're doing here Me: We've been doing problems on de Morgan's rule--see page 24 Steve: ok, thanks Me: Okay--let's go back to Janell's question. Scroll up and take a look. Me: Can somebody tell us what characterizes associativity? It's true in logic and ordinary algebra. Me: Mark, wanna take a shot at it? Mark: both sides of the equation are equal? Janet: they can be flip to equal the other side Me: Important point--for each of these, it's two ways of writing the same thing. Me: And so you can flip them around, yes. What else? Steve? Me: Take a look at the parentheses in the associative law. Steve: they can be switched around Janet: something about the first letter being the parentheses Me: exactly--associativity means moving around parenthesees Me: Now compare this to the commutative laws...Kate--what's the difference? Kate: im not sure Janet: would you be moving the letters Me: Okay--notice there aren't any parentheses to move, right? Janet: yes Me: So what moves? Janet: the letter Janet: or is it the sign Me: Right--the variables change sides. Janet: is that true for all the cases? Me: So, associativity = moving parentheses, commutativity = moving variables. Me: Yes, it's always true. Janet: ok |







No comments:
Post a Comment